黄金比

黄金比とは

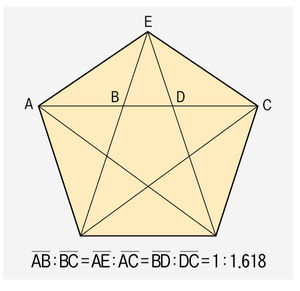
ギリシャの数学者ピタゴラスが人間が思う最も安定して、美しい比率を考案中、黄金比を作りました。当時、ピタゴラス学派のシンボルの正五角形がまさにこの黄金比を参考したものです。

出典：https://blog.naver.com/mathfirstacademy/221158125089

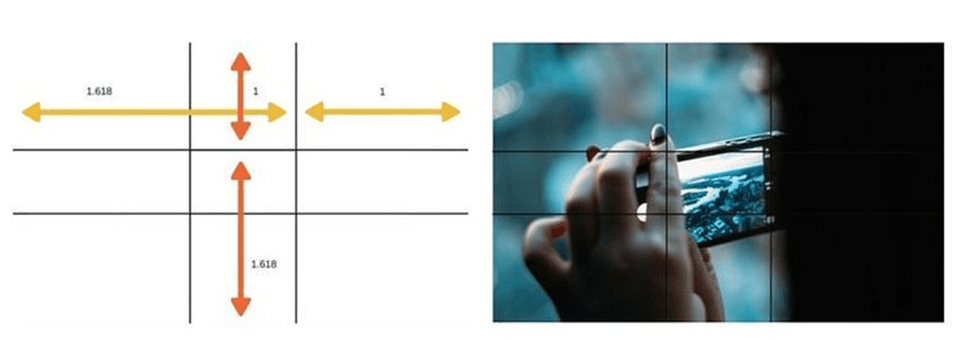
なぜ黄金比は安定感があるように見えるか？

フィボナッチ数列

レオナルド フィボナッチ

レオナルド フィボナッチ （1170年頃 - 1250年頃）は、中世で最も才能があったと評価されるイタリアの数学者。 本名はレオナルド・ダ・ピサ（ピサのレオナルド）という。フィボナッチは「ボナッチの息子」を意味する愛称だが、19世紀の数学史家リブリが誤って作った名前でもある。
フィボナッチは、近代では主に次のような業績で知られている。
13世紀初頭に、『算盤の書』の出版を通じてアラビア数字のシステムをヨーロッパに導入した。
自身で発見したわけではないが、『算盤の書』の中で例として紹介したことで、「フィボナッチ数列」に名前を残した。

出典：https://blog.naver.com/mathfirstacademy/221158125089

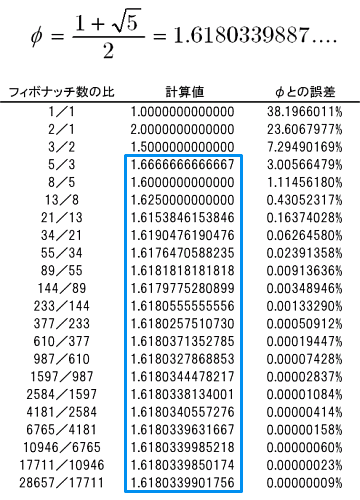
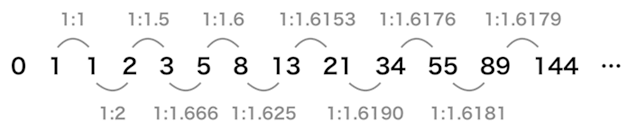
フィボナッチ数列は、「2つ前の項と1つ前の項を足し合わせていくことでできる数列」のことです。数列は「1,1」から始まり、
1, 1, 2, 3, 5, 8, 13, 21…と続いていきます。
これを式ですると、

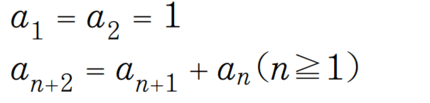
出典：studyplus

となります。これがフィボナッチ数列です。

問題

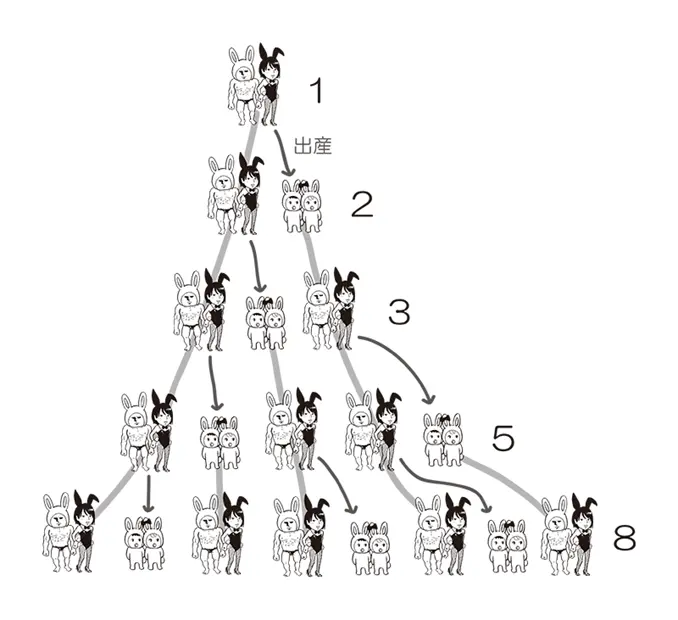
「１つがいのウサギは、産まれて２か月目から毎月１つがいのウサギを産む。１つがいのウサギは１年の間に何つがいのウサギになるか？　ただし、どのウサギも死なないものとする。」

出典：http://www.studio-ggy.com/math/2013/04/21--.html

出典：シルバニアファミリー

正解は「144」づがいになる。（正解はマウスでDragしてください。）

フィボナチ数列と黄金比の関連性

出典：http://oto-suu.seesaa.net/article/243870124.html

フィボナチ数列を計算式を見ると黄金比の比率と似てる。

自然界の不思議な法則 -フィボナッチ数列

ひまわりの螺旋を見るとフィボナチ数列のことがわかる。

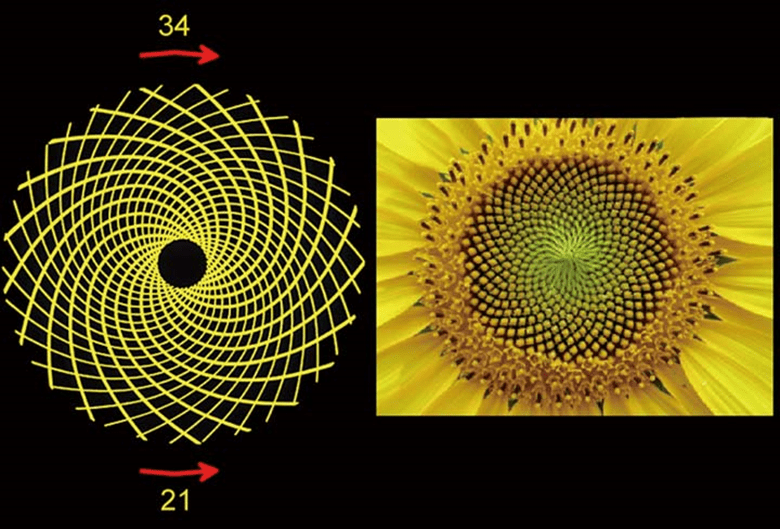
出典：https://blog.naver.com/mathfirstacademy/221158125089

自然界 ≒ フィボナチ数列 ≒ 黄金比

自然界と似ているので人間は黄金比に安定感を感じてるのではないでしょうか？

黄金比の使い方の例

黄金比をレイアウトに使ってみましょう。

出典：Photography Mad

テキストエリアを1、画像を1.618にして黄金比に合わせた。

出典：Creative Blog

テキストエリアと顔を横に少しずらして黄金比に合わせた。

出典：Feld Magazine

黄金比を使ったレイアウト。

出典：Moodley

使用実例

名刺のレイアウトと余白を黄金比で使った。